Chapter 5 Using the OpenMx Package for CFA
The OpenMX package in R is a port of the well-respected MX analytical software. It handles SEM and can easily be used for CFA. Here, the same two models that were run in lavaan will be run again, but an additional model will be run first.
library(OpenMx)5.1 First OpenMx Model - Single Factor
First, fit a bad model that posits only one underlying factor
5.1.1 set new dataframe and set up basics
Some initial setups
# grab data
#wisc2 <- wisc1[2:12] # remove ID from df
# set up basics
manifests=names(wisc2)
observedCov <- cov(wisc2)
numSubjects <- nrow(wisc2)5.1.2 Create the model using the mxModel function
This code initializes the model and sets vars/paths
latents="F1"
cfa2a <- mxModel("Common Factor Model",type="RAM",
manifestVars = manifests, latentVars = latents,
# Now set the residual variance for manifest variables
mxPath(from=manifests, arrows=2,free=T,values=1,labels=paste("error",1:11,sep="")),
# set latent factor variance to 1
mxPath(from="F1",arrows=2,free=F,values=1,labels="varF1"),
# specify factor loadings
mxPath(from="F1",to=manifests, arrows=1,
free=T,values=1,labels=paste("i", 1:11,sep="")),
# specify the covariance matrix
mxData(observed=observedCov,type="cov",numObs=numSubjects)
) # close the model5.1.3 Now use mxRun to fit the model
mxRun uses the model defined above.
cfa2a <- mxRun(cfa2a)## Running Common Factor Model with 22 parametersSummarize the fit:
summary(cfa2a)## Summary of Common Factor Model
##
## free parameters:
## name matrix row col Estimate Std.Error A
## 1 i1 A info F1 2.10843 0.20489
## 2 i2 A comp F1 2.10258 0.20876
## 3 i3 A arith F1 1.27253 0.17310
## 4 i4 A simil F1 2.25978 0.22323
## 5 i5 A vocab F1 2.17498 0.20342
## 6 i6 A digit F1 1.00892 0.21308
## 7 i7 A pictcomp F1 1.35055 0.22867
## 8 i8 A parang F1 0.89834 0.21227
## 9 i9 A block F1 1.23160 0.21130
## 10 i10 A object F1 1.01784 0.22717
## 11 i11 A coding F1 0.20128 0.23480
## 12 error1 S info info 3.98738 0.54543
## 13 error2 S comp comp 4.32199 0.56950
## 14 error3 S arith arith 3.67209 0.42704
## 15 error4 S simil simil 4.97100 0.64992
## 16 error5 S vocab vocab 3.82117 0.53031
## 17 error6 S digit digit 6.25280 0.68878
## 18 error7 S pictcomp pictcomp 6.73647 0.76246
## 19 error8 S parang parang 6.22646 0.68288
## 20 error9 S block block 5.78440 0.65307
## 21 error10 S object object 7.00600 0.77245
## 22 error11 S coding coding 8.16142 0.87333
##
## Model Statistics:
## | Parameters | Degrees of Freedom | Fit (-2lnL units)
## Model: 22 44 5492.0
## Saturated: 66 0 5375.1
## Independence: 11 55 5894.3
## Number of observations/statistics: 175/66
##
## chi-square: <U+03C7>² ( df=44 ) = 116.85, p = 1.5993e-08
## Information Criteria:
## | df Penalty | Parameters Penalty | Sample-Size Adjusted
## AIC: 28.851 160.85 167.51
## BIC: -110.400 230.48 160.81
## CFI: 0.84306
## TLI: 0.80383 (also known as NNFI)
## RMSEA: 0.097268 [95% CI (0.071763, 0.12282)]
## Prob(RMSEA <= 0.05): 0.00026603
## timestamp: 2019-07-11 11:27:01
## Wall clock time: 0.08 secs
## optimizer: CSOLNP
## OpenMx version number: 2.12.2
## Need help? See help(mxSummary)What is in the model?
slotNames(cfa2a@output)## NULLnames(cfa2a@output)## [1] "matrices" "algebras"
## [3] "data" "SaturatedLikelihood"
## [5] "IndependenceLikelihood" "calculatedHessian"
## [7] "standardErrors" "gradient"
## [9] "hessian" "expectations"
## [11] "fit" "fitUnits"
## [13] "Minus2LogLikelihood" "maxRelativeOrdinalError"
## [15] "minimum" "estimate"
## [17] "infoDefinite" "conditionNumber"
## [19] "status" "iterations"
## [21] "evaluations" "mxVersion"
## [23] "frontendTime" "backendTime"
## [25] "independentTime" "wallTime"
## [27] "timestamp" "cpuTime"5.2 Second OpenMx Model - the bifactor model
Now fit a model that is the same as the initial model fit with lavaan in chapter 3. Two factors, verbal and performance are established with each manifest variable uniquely specified by only one of the two latent factors.
5.2.1 set new dataframe and set up basics
Same initial setups as above.
# grab data
wisc2 <- wisc1[2:12] # remove ID from df
# set up basics
manifests <- names(wisc2)
verbalVars <- names(wisc2[1:6])
perfVars <- names(wisc2[7:11])
latents2 <- c("verbal","perf")
#manifests <- c("verbalVars","perfVars")
observedCov <- cov(wisc2[,1:11])
numSubjects <- nrow(wisc2)5.2.2 Create the model using the mxModel function
Essentially initializes the model and sets vars/paths
cfa2b <- mxModel("Two Factor Model",type="RAM",
manifestVars = manifests, latentVars = latents2,
# Now set the residual variance for manifest variables
mxPath(from = manifests, arrows=2,free=T,values=1, labels=paste("e",1:11,sep="")),
# set latent factor variances
mxPath(from=latents2,arrows=2,free=F,values=1,labels=c("p1","p2")),
# speciffy factor loadings
# Allow the factors to covary as per the lavaan model
mxPath(from="verbal", to="perf", arrows=2,
free=T, values=1, labels="latcov1"),
# Specify the latent factor paths to manifests
mxPath(from="verbal", to = verbalVars,
arrows=1,
free=T,values=1),
mxPath(from="perf", to = perfVars,
arrows=1,
free=T,values=1),
mxData(observed=observedCov,type="cov",numObs=numSubjects)
) # close the model5.2.3 Now use ’mxRun’to fit the model
mxRun uses the model defined above
cfa2b <- mxRun(cfa2b)## Running Two Factor Model with 23 parametersSummarize the fit
summary(cfa2b)## Summary of Two Factor Model
##
## free parameters:
## name matrix row col Estimate Std.Error A
## 1 Two Factor Model.A[1,12] A info verbal 2.20616 0.201309
## 2 Two Factor Model.A[2,12] A comp verbal 2.04220 0.211937
## 3 Two Factor Model.A[3,12] A arith verbal 1.29984 0.172679
## 4 Two Factor Model.A[4,12] A simil verbal 2.23205 0.225198
## 5 Two Factor Model.A[5,12] A vocab verbal 2.25045 0.200598
## 6 Two Factor Model.A[6,12] A digit verbal 1.05277 0.212308
## 7 Two Factor Model.A[7,13] A pictcomp perf 1.74200 0.246173
## 8 Two Factor Model.A[8,13] A parang perf 1.25323 0.224773
## 9 Two Factor Model.A[9,13] A block perf 1.84593 0.224562
## 10 Two Factor Model.A[10,13] A object perf 1.60457 0.236048
## 11 Two Factor Model.A[11,13] A coding perf 0.20701 0.257118
## 12 e1 S info info 3.56570 0.516752
## 13 e2 S comp comp 4.57229 0.594874
## 14 e3 S arith arith 3.60184 0.422011
## 15 e4 S simil simil 5.09555 0.666203
## 16 e5 S vocab vocab 3.48717 0.507536
## 17 e6 S digit digit 6.16241 0.680961
## 18 e7 S pictcomp pictcomp 5.52590 0.772061
## 19 e8 S parang parang 5.46287 0.658943
## 20 e9 S block block 3.89376 0.651701
## 21 e10 S object object 5.46733 0.719732
## 22 e11 S coding coding 8.15907 0.874195
## 23 latcov1 S verbal perf 0.58883 0.077178
##
## Model Statistics:
## | Parameters | Degrees of Freedom | Fit (-2lnL units)
## Model: 23 43 5445.7
## Saturated: 66 0 5375.1
## Independence: 11 55 5894.3
## Number of observations/statistics: 175/66
##
## chi-square: <U+03C7>² ( df=43 ) = 70.608, p = 0.0050089
## Information Criteria:
## | df Penalty | Parameters Penalty | Sample-Size Adjusted
## AIC: -15.392 116.61 123.92
## BIC: -151.478 189.40 116.56
## CFI: 0.94053
## TLI: 0.92393 (also known as NNFI)
## RMSEA: 0.060571 [95% CI (0.026575, 0.089595)]
## Prob(RMSEA <= 0.05): 0.23348
## timestamp: 2019-07-11 11:27:02
## Wall clock time: 0.0754 secs
## optimizer: CSOLNP
## OpenMx version number: 2.12.2
## Need help? See help(mxSummary)What is in the model?
slotNames(cfa2b@output)## NULLnames(cfa2b@output)## [1] "matrices" "algebras"
## [3] "data" "SaturatedLikelihood"
## [5] "IndependenceLikelihood" "calculatedHessian"
## [7] "standardErrors" "gradient"
## [9] "hessian" "expectations"
## [11] "fit" "fitUnits"
## [13] "Minus2LogLikelihood" "maxRelativeOrdinalError"
## [15] "minimum" "estimate"
## [17] "infoDefinite" "conditionNumber"
## [19] "status" "iterations"
## [21] "evaluations" "mxVersion"
## [23] "frontendTime" "backendTime"
## [25] "independentTime" "wallTime"
## [27] "timestamp" "cpuTime"5.2.4 Can we use semPlot to draw the OpenMx model fit?
The semPlot package is very powerful and can recognize many lm and sem model objects. We can use the identical code that we used in chapter 2 for the lavaan model.
# Note that the base plot, including standardized path coefficients plots positive coefficients green
# and negative coefficients red. Red-green colorblindness issues anyone?
# I redrew it here to choose a blue and red. But all the coefficients in this example are
# positive,so they are shown with the skyblue.
# more challenging to use colors other than red and green. not in this doc
semPaths(cfa2b, residuals=F,sizeMan=7,"std",
posCol=c("skyblue4", "red"),
#edge.color="skyblue4",
edge.label.cex=1.2,layout="circle2")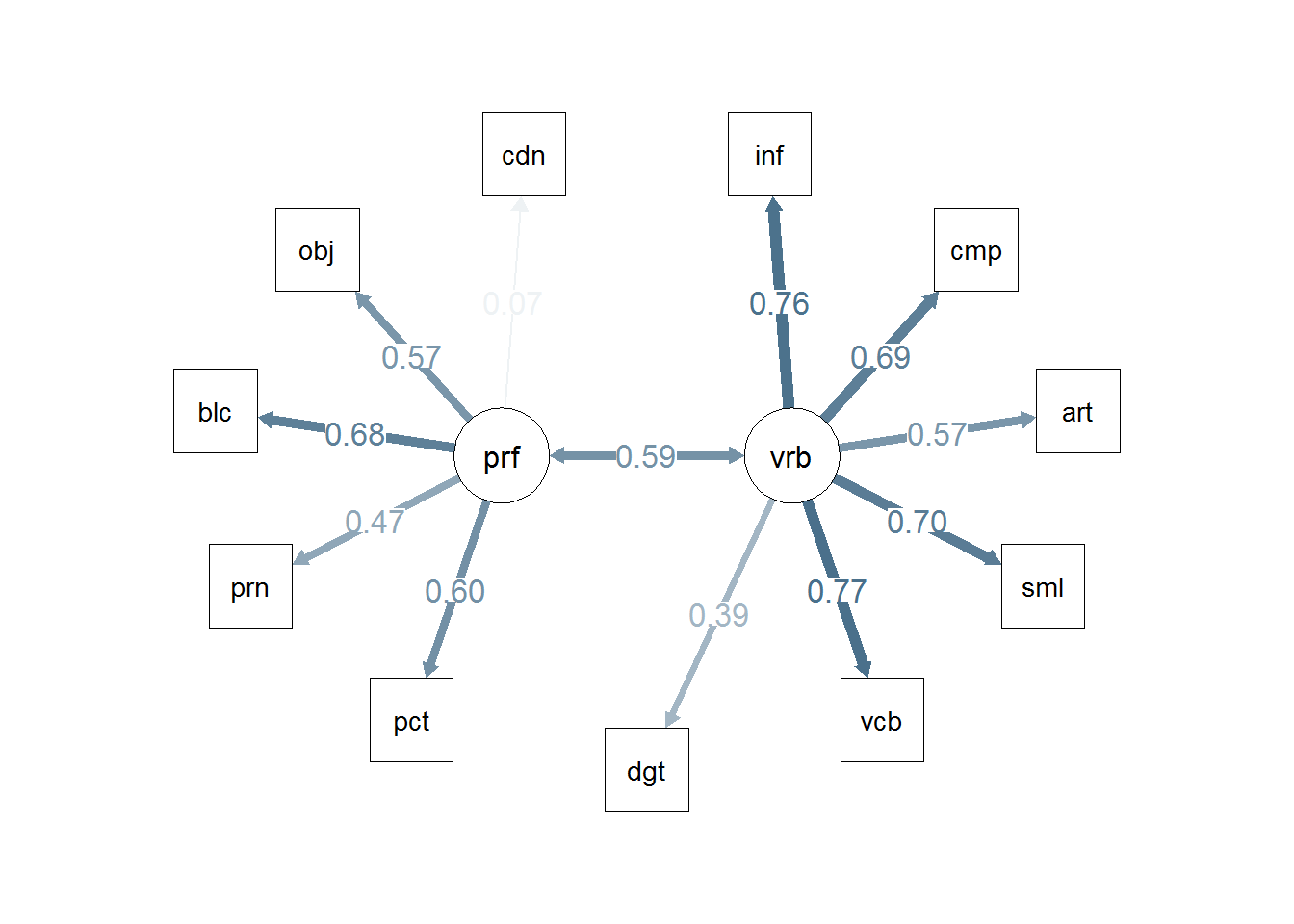
# or we could draw the paths in such a way to include the residuals:
#semPaths(fit1, sizeMan=7,"std",edge.color="skyblue4",edge.label.cex=1,layout="circle2")
# the base path diagram can be drawn much more simply:
#semPaths(fit1)
# or
semPaths(cfa2b,"std")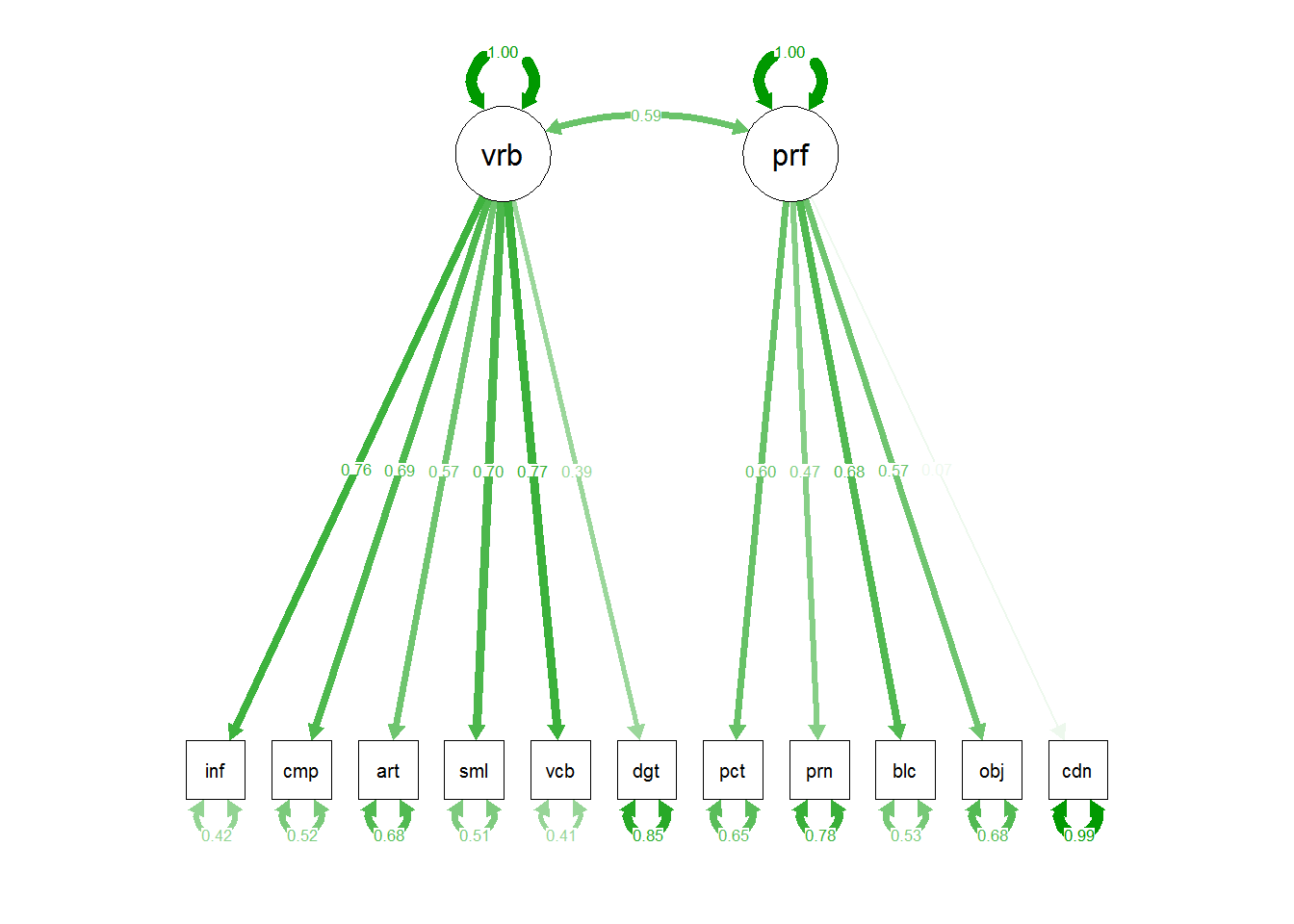
5.3 Third OpenMx Model
Now fit a model that is the same as the second model fit with lavaan above. Two factors, verbal and performance, plus paths from both latents to “comp”.
5.3.1 set new dataframe and set up basics
Same initial setups as above.
# grab data
wisc2 <- wisc1[2:12] # remove ID from df
# set up basics
manifests <- names(wisc2)
verbalVars <- names(wisc2[1:6])
perfVars <- c(names(wisc2[7:11]),"comp")
latents2 <- c("verbal","perf")
#manifests <- c("verbalVars","perfVars")
observedCov <- cov(wisc2[,1:11])
numSubjects <- nrow(wisc2)5.3.2 Create the model using the mxModel function
Essentially initializes the model and sets vars/paths
cfa2c <- mxModel("TwoFac, Comp Common",type="RAM",
manifestVars = manifests, latentVars = latents2,
# Now set the residual variance for manifest variables
mxPath(from = manifests, arrows=2,free=T,values=1, labels=paste("e",1:11,sep="")),
# set latent factor variances
mxPath(from=latents2,arrows=2,free=F,values=1,labels=c("p1","p2")),
# speciffy factor loadings
# Allow the factors to covary as per the lavaan model
mxPath(from="verbal", to="perf", arrows=2,
free=T, values=1, labels="latcov1"),
# Specify the latent factor paths to manifests
mxPath(from="verbal", to = verbalVars,
arrows=1,
free=T,values=1),
mxPath(from="perf", to = perfVars,
arrows=1,
free=T,values=1),
mxData(observed=observedCov,type="cov",numObs=numSubjects)
) # close the model5.3.3 Now use ‘mxRun’ to fit the model
mxRun uses the model defined above
cfa2c <- mxRun(cfa2c)## Running TwoFac, Comp Common with 24 parametersSummarize the fit
summary(cfa2c)## Summary of TwoFac, Comp Common
##
## free parameters:
## name matrix row col Estimate
## 1 TwoFac, Comp Common.A[1,12] A info verbal 2.25606
## 2 TwoFac, Comp Common.A[2,12] A comp verbal 1.49130
## 3 TwoFac, Comp Common.A[3,12] A arith verbal 1.30678
## 4 TwoFac, Comp Common.A[4,12] A simil verbal 2.20475
## 5 TwoFac, Comp Common.A[5,12] A vocab verbal 2.27348
## 6 TwoFac, Comp Common.A[6,12] A digit verbal 1.07476
## 7 TwoFac, Comp Common.A[2,13] A comp perf 0.88414
## 8 TwoFac, Comp Common.A[7,13] A pictcomp perf 1.78962
## 9 TwoFac, Comp Common.A[8,13] A parang perf 1.18881
## 10 TwoFac, Comp Common.A[9,13] A block perf 1.82276
## 11 TwoFac, Comp Common.A[10,13] A object perf 1.63283
## 12 TwoFac, Comp Common.A[11,13] A coding perf 0.20047
## 13 e1 S info info 3.34302
## 14 e2 S comp comp 4.33109
## 15 e3 S arith arith 3.58375
## 16 e4 S simil simil 5.21667
## 17 e5 S vocab vocab 3.38297
## 18 e6 S digit digit 6.11561
## 19 e7 S pictcomp pictcomp 5.35770
## 20 e8 S parang parang 5.62019
## 21 e9 S block block 3.97877
## 22 e10 S object object 5.37584
## 23 e11 S coding coding 8.16174
## 24 latcov1 S verbal perf 0.53322
## Std.Error A
## 1 0.200315
## 2 0.256354
## 3 0.173048
## 4 0.227320
## 5 0.200572
## 6 0.212373
## 7 0.270140
## 8 0.242338
## 9 0.225100
## 10 0.221685
## 11 0.233235
## 12 0.255009
## 13 0.509394
## 14 0.557177
## 15 0.422007
## 16 0.682585
## 17 0.507400
## 18 0.677590
## 19 0.755634
## 20 0.665637
## 21 0.636905
## 22 0.708170
## 23 0.874112
## 24 0.082033
##
## Model Statistics:
## | Parameters | Degrees of Freedom | Fit (-2lnL units)
## Model: 24 42 5435.7
## Saturated: 66 0 5375.1
## Independence: 11 55 5894.3
## Number of observations/statistics: 175/66
##
## chi-square: <U+03C7>² ( df=42 ) = 60.61, p = 0.031396
## Information Criteria:
## | df Penalty | Parameters Penalty | Sample-Size Adjusted
## AIC: -23.39 108.61 116.61
## BIC: -156.31 184.56 108.56
## CFI: 0.95991
## TLI: 0.9475 (also known as NNFI)
## RMSEA: 0.050319 [95% CI (0, 0.081389)]
## Prob(RMSEA <= 0.05): 0.4664
## timestamp: 2019-07-11 11:27:07
## Wall clock time: 0.029 secs
## optimizer: CSOLNP
## OpenMx version number: 2.12.2
## Need help? See help(mxSummary)What is in the model?
slotNames(cfa2c@output)## NULLnames(cfa2c@output)## [1] "matrices" "algebras"
## [3] "data" "SaturatedLikelihood"
## [5] "IndependenceLikelihood" "calculatedHessian"
## [7] "standardErrors" "gradient"
## [9] "hessian" "expectations"
## [11] "fit" "fitUnits"
## [13] "Minus2LogLikelihood" "maxRelativeOrdinalError"
## [15] "minimum" "estimate"
## [17] "infoDefinite" "conditionNumber"
## [19] "status" "iterations"
## [21] "evaluations" "mxVersion"
## [23] "frontendTime" "backendTime"
## [25] "independentTime" "wallTime"
## [27] "timestamp" "cpuTime"5.3.4 Draw the OpenMx model number 3
The semPlot package is very powerful and can recognize many ‘lm’ and SEM model objects. We can use the identical code that we used in chapter 2 for the lavaan model.
# Note that the base plot, including standardized path coefficients plots positive coefficients green
# and negative coefficients red. Red-green colorblindness issues anyone?
# I redrew it here to choose a blue and red. But all the coefficients in this example are
# positive,so they are shown with the skyblue.
# more challenging to use colors other than red and green. not in this doc
semPaths(cfa2c, residuals=F,sizeMan=7,"std",
posCol=c("skyblue4", "red"),
#edge.color="skyblue4",
edge.label.cex=1.2,layout="circle2")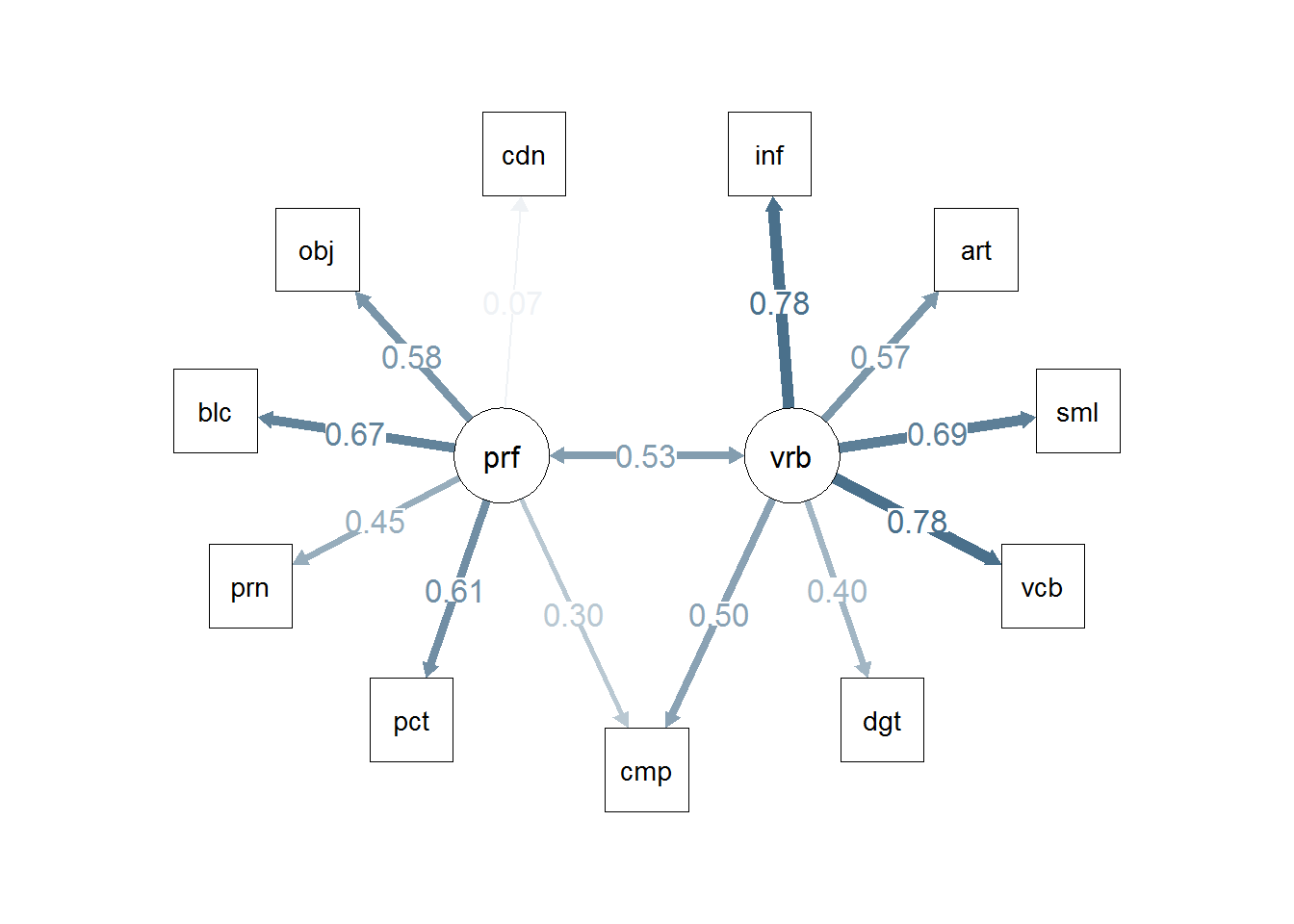
# or we could draw the paths in such a way to include the residuals:
#semPaths(fit1, sizeMan=7,"std",edge.color="skyblue4",edge.label.cex=1,layout="circle2")
# the base path diagram can be drawn much more simply:
#semPaths(fit1)
# or
semPaths(cfa2c,"std")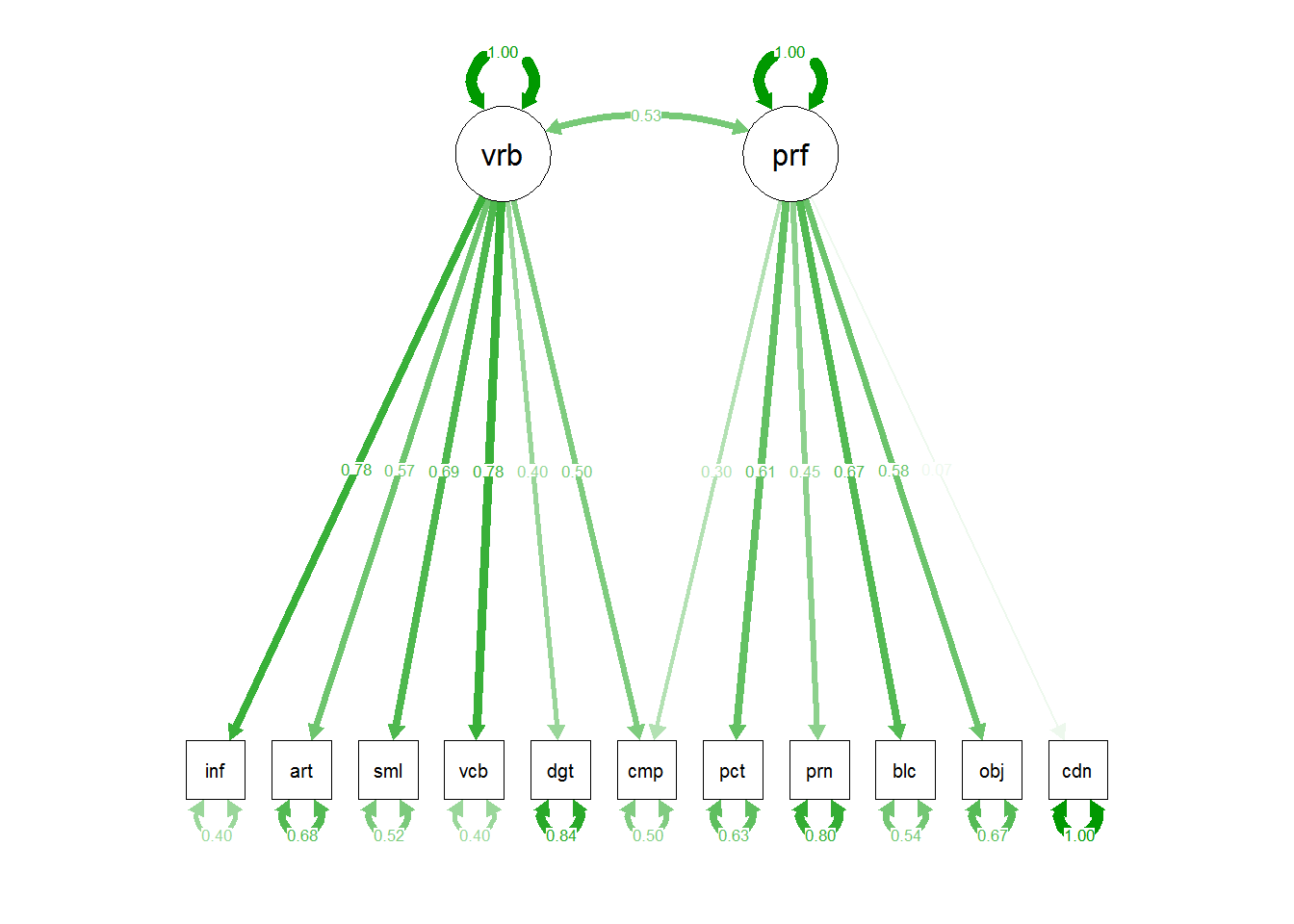
5.4 Compare the OpenMx models
In OpenMx a convenient function exists for model comparisons. This code compares the same two models that we initially compared in the lavaan approach that used the anova function.
kable(mxCompare(cfa2c,cfa2b), booktabs=TRUE, format="markdown")| base | comparison | ep | minus2LL | df | AIC | diffLL | diffdf | p |
|---|---|---|---|---|---|---|---|---|
| TwoFac, Comp Common | NA | 24 | 5435.7 | 42 | -23.390 | NA | NA | NA |
| TwoFac, Comp Common | Two Factor Model | 23 | 5445.7 | 43 | -15.392 | 9.998 | 1 | 0.00157 |